Finding f with a Macro Lens

The Method

We start with equations (5) and (6) as derived on the leading page.

      1       1     1
    ----- + ----- = -                        (5)
    a + b   c + d   f


        c + d
    M = -----                                (6)
        a + b

Then we express c + d from (6), substitute into (5), and solve for f:

    c + d = M (a + b)


    1     1       1
    - = ----- + -----                        <=>
    f   a + b   c + d


    1     1         1
    - = ----- + ---------                    <=>
    f   a + b   M (a + b)


    1     M + 1
    - = ---------                             =>
    f   M (a + b)


    f (M + 1) = M (a + b)                    (7)

The unknowns here are M, a, and b. M is easy — we use a macro lens, and read it right off the lens barrel.

To find out a, we proceed as follows:

1. Mount the lens on a camera body.
2. Turn the lens focusing ring to a freely chosen magnification ratio M.
3. Focus on an object by moving the lens-camera combo back and forth.
4. Measure the distance a between the object and the front-most point of the lens.

For b we perform these further steps:

1. Find a dark distant object in front of a bright background (for example a distant tree in front of a sunrise or a sunset).
2. Without refocusing the lens, take it off the camera, and point its rear element towards the object.
3. Place a white piece of paper behind the front element of the lens. Use the paper as a screen to project an image with the lens.
4. Move the paper back and forth until the image of the distant tree is in focus.
5. Measure the distance d between the front-most point of the lens filter thread and the paper.

Figure 1 illustrates.

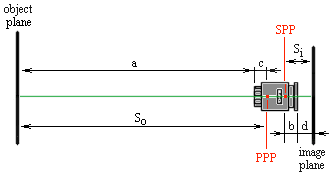
Figure 1.

Now we see how to calculate b from d. We start again with equation (5), but because the lens is used backwards, and because of the equation’s symmetry, b and c swap their positions. So (5) becomes:

      1       1     1
    ----- + ----- = -                        (8)
    a + c   b + d   f

Now comes the approximation — we assume that the distance to the object (the tree) is equal to infinity. Equation (8) then simplifies to:

        1        1     1
    -------- + ----- = -                     <=>
    infinity   b + d   f


      1     1
    ----- = -                                <=>
    b + d   f


    f = b + d                                <=>


    b = f - d                                (9)

Now we substitute (9) into (7), and solve for f:

    f (M + 1) = M (a + f - d)                <=>


    fM + f = fM + M (a - d)                  <=>


    f = M (a - d).

Method Evaluation

The two main merits of this method are:

1. Simplicity, both experimental and mathematical.
2. High tolerance to measurement errors. We measure the quantities a and d, and their dependance to f is linear. Second, we are free to choose M, and for smaller values, the effect of any measurement errors decreases.

At the same time, three main drawbacks should be pointed out:

1. Because the method assumes that the distant object lies at infinity, the result is only approximate. The ill-effects of this approximation are very small, however. For example, for a 100 mm lens and an object located 20 meters away instead of at infinity, the maximum error in f is 0.5 millimeters (for M = 1:1, smaller for smaller values of M).
2. The method is directly applicable only for lenses that have the magnification ratio marked on the barrel. It can be applied to any lens, but then M must be calculated in a separate experiment.
3. The method finds the focal length only for the chosen M. In general this is no limitation, as most lenses retain a constant f as they are refocused. For those that do change f, the method can be applied a number of times to get an idea of how f changes. The method fails for one important case, however, when the lens is focused at infinity (M = 0). This is so because M is present in the final expression for f.